4 Infinite Time Turing Machines
First introduced by Hamkins and Lewis in 1998 (Hamkins and Lewis 2000), ITTMs extend the classical Turing Machine by incorporating transfinite ordinal time steps. This theoretical advancement allows ITTMs to perform computations beyond the finite operations of traditional Turing Machines, enabling them to address problems that are undecidable within the conventional framework of computation.
By executing an infinite sequence of steps and leveraging specialized mechanisms to determine states at transfinite stages, ITTMs transcend the limits of finite computation. This capability allows them to process infinite sequences, resolve undecidable problems like the Halting Problem for classical Turing Machines, and explore the realm of hypercomputation.
In this section, we build on the computational hierarchy discussed in Section 2.3 to provide an intuitive and formal understanding of ITTMs. To begin, we will develop intuition around the concept of computing with infinity—examining how infinite steps and transfinite reasoning can be used to achieve well-defined computational outcomes. From there, we will explore the specifics of ITTMs, defining their operation, mechanisms, and the remarkable problems they can solve, and situating them as a fundamental expansion of what is computationally possible.
4.1 Example: Computing with Infinity
To illustrate the concept of leveraging infinite steps for computation, consider the following example:
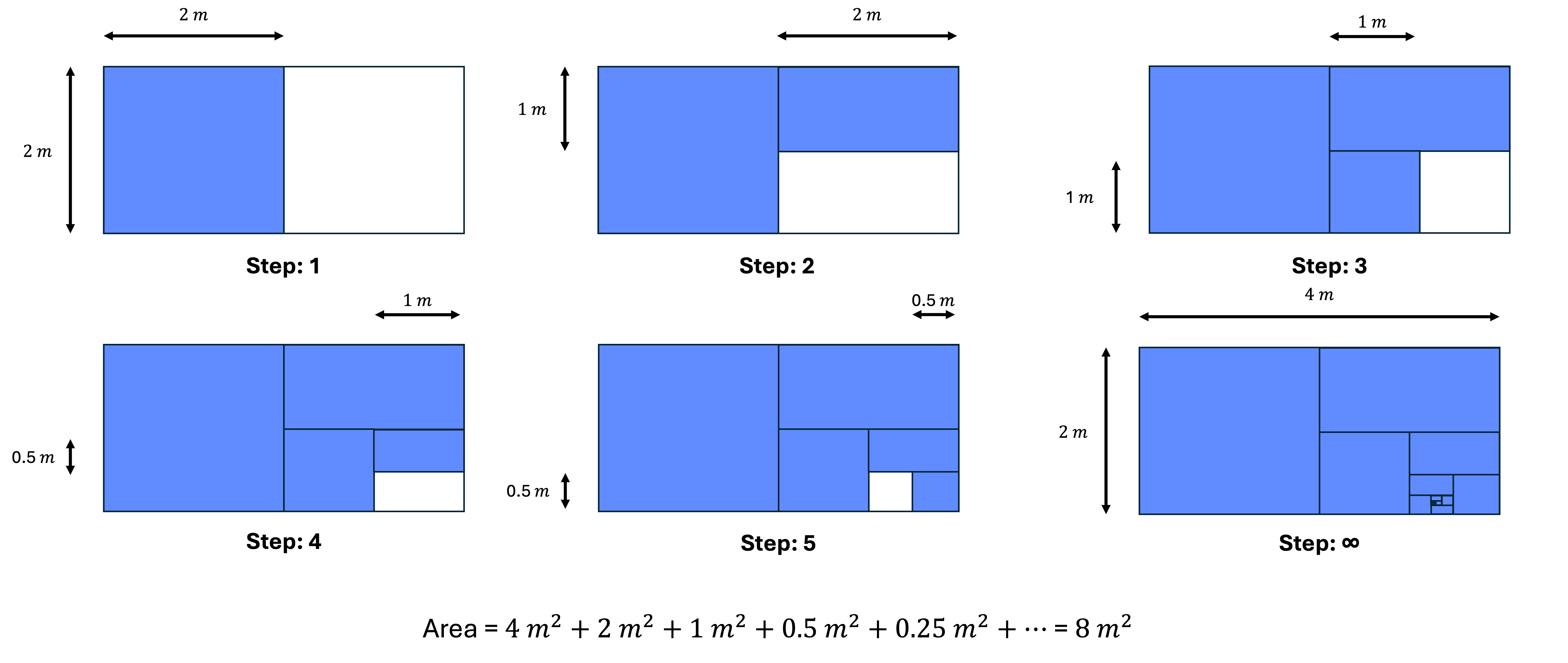
Given a rectangle with a height of \(2 \, m^2\) and a width of \(4 \, m^2\), we can calculate its area to be \(8 \, m^2\).
However, this is not the only approach we can use to perform this computation. Consider another; an iterative approach, whereby we bisect the shape into successively smaller pieces, halving the previous piece at each step to approach the true answer by iteration.
As illustrated in Figure 4.1, we can see that the iterative approach converges to the correct answer of \(8 \, m^2\). However, when we consider the number of steps taken to compute this answer, we find that it is infinite.
This is an example of a computation that required an infinite number of steps, but has a definite, finite answer. This concept of computing with infinity is at the heart of ITTMs.
4.2 Infinite Successor Ordinals
To understand how ITTMs leverage computation after performing countably infinite steps, we must first define a system for indexing time steps past infinity. Infinite successor ordinals provide a way to do this by extending the concept of ordinal numbers to include, and go beyond a notion of infinity.
First, consider a machine \(M\) that has machine state \(s_t\) at time step \(t\). Note that this machine, unlike the Turing Machines we saw previously, has the ability to take a state at time steps beyond infinity.
Combining this with our notion of representing a Turing Machine evolving through time (see Section 3.4 and Figure 3.3), we can define the machine state at time step \(\omega\) as \(s_\omega\). Note that the difference between this notation and the indexing notation used in Figure 4.1 is that instead of using \(\infty\), we use \(\omega\) to represent the first infinite ordinal.

We can extend this notion of ascribing state \(s_\omega\) to the machine at time step \(\omega\) by considering additional successor ordinals beyond the first infinite successor ordinal \(\omega\), such as \(\omega + 1\), \(\omega + 2\), and so on. Correspondingly, the machine state at time step \(\omega + 1\) would be \(s_{\omega + 1}\), and so forth.
This extension allows us to represent the machine’s state at countably infinite time steps, providing a framework for indexing ITTMs at, and beyond the first infinite ordinal \(\omega\). This concept is illustrated in Figure 4.2.
4.3 Defining an Infinite Time Turing Machine
An Infinite Time Turing Machine is a theoretical computational model that extends the operation of a classical Turing machine into transfinite ordinal time steps. In this model, computations proceed through an infinite sequence of steps, including limit ordinals. At these limit stages, the machine’s state and tape configurations are determined by taking the “limit” of all preceding states and tape contents. This extension allows ITTMs to perform computations beyond the capabilities of standard Turing machines, such as solving the halting problem for ordinary Turing machines. That is, an ITTM is a machine that can perform computations after performing countably infinite steps of computation. This is achieved by defining the machine’s behavior at and beyond the first infinite ordinal time step, \(\omega\).
The state of the machine at each time step is the result of a limit supremum calculation, and is contingent on previous tape states.
Formally, for a machine \(M\), cell \(k\), and a limit ordinal \(\lambda\), then:
\[ T(\lambda)_k = \limsup_{n \rightarrow \lambda} \left( T(n)_k \right) \]
The limit supremum plays a pivotal role in defining the state of an ITTM at limit ordinal time steps, such as \(\omega\), where computation transitions from finite sequences to transfinite stages. At these limit points—where no immediate predecessor exists—the machine determines its state and tape contents based on the “dominant” behavior of preceding configurations. If a particular cell stabilizes to a single value as the computation progresses toward a limit ordinal, that value is adopted. In cases where the cell oscillates without convergence, predefined rules resolve the ambiguity, ensuring a well-defined computational outcome.
This mechanism can be likened to optimization processes in deep learning, particularly in constrained convergence scenarios. For example, when training a model over mini-batches, deep learning frameworks iteratively adjust weights by averaging gradients while respecting constraints imposed by the global loss function. Similarly, the limit supremum in ITTMs acts as a constrained resolution mechanism, balancing the sequential operations on the tape with the ordinal indexing of computation steps. Both processes share the principle of leveraging cumulative behaviors to determine stable, interpretable outcomes at critical points.
4.3.1 Transcending the Limits of Classical Computation
ITTMs surpass classical Turing Machines by extending computation into the transfinite, allowing them to solve problems that are inherently undecidable in the finite framework of classical computation. By introducing the concept of limit ordinals and successor stages, ITTMs redefine what it means to compute, enabling operations that leverage the cumulative behavior of infinite sequences.
4.4 Hypercomputation
Beyond this, ITTMs provide a framework for solving a broader class of problems classified as hypercomputations (Copeland 2002). These are tasks that extend beyond the reach of finite-state machines, including the analysis of infinite-state systems and problems requiring transfinite reasoning. The ability to perform such computations stems directly from ITTMs’ capacity to transition seamlessly between finite and transfinite ordinal steps, making them uniquely equipped to model processes involving infinite or unbounded complexity.
This remarkable expansion of computational boundaries not only challenges our understanding of what machines can achieve but also invites new inquiries into the implications of transfinite computation. To explore this further, we delve into the concept of hypercomputation, formalizing the kinds of problems ITTMs can address and the theoretical implications of their extended capabilities.
Formally, Hypercomputation can be defined as:
Hypercomputation refers to computations that go beyond the limits of what Turing machines can solve, potentially using infinite time or other methods.
Perhaps most notably, an example of a Hypercomptuation is solving the Turing Machine Halting Problem.
4.4.1 Solving the Turing Machine Halting Problem
The Turing Halting Problem is a fundamental question in computer science that asks whether it is possible to design an algorithm that can determine, for any given Turing machine and input, whether the machine will eventually halt or continue running indefinitely. Alan Turing proved that a general solution to this problem is impossible because there is no algorithm that can correctly predict the behavior of all Turing machines. This limitation highlights the boundaries of computability within the framework of classical computation, demonstrating that there exist certain problems that no standard Turing machine can solve.
One of the clearest demonstrations of this power is ITTMs’ ability to address the Halting Problem for classical Turing Machines. At transfinite stages, ITTMs determine whether a computation halts by evaluating its “limit state,” a synthesis of all prior configurations. Using the limit supremum to stabilize or resolve oscillatory behaviors, ITTMs achieve clarity at points where classical computation breaks down.
At these limit stages, the ITTM evaluates the entire infinite sequence of configurations and stabilizes at a new state. By continuing computations through this process, an ITTM can determine if a standard Turing machine halts by examining whether it reaches a final, stable configuration after this extended series of operations. Thus, an ITTM resolves the halting problem for conventional Turing machines by effectively computing over an infinite timeline.
This approach effectively bypasses the finite constraints that make the Halting Problem undecidable for classical machines, offering a profound extension to the concept of computability.
4.4.2 Cognitive Processes as Hypercomputation
We assert that human cognitive processes — including complex tasks like fine motor control, problem-solving, intuitive decision-making, and language comprehension — function as forms of hypercomputation. This claim is grounded in Roger Penrose’s descriptions of non-computable cognitive activities and aligns with the formal definition of hypercomputation developed later. In Shadows of the Mind (Penrose 1994), Penrose argues that human consciousness and understanding involve reasoning and comprehension that go beyond what is possible with Turing-computable algorithms. He draws parallels between various advanced cognitive tasks, suggesting that all involve the recognition of truths and actions inaccessible to purely algorithmic systems.
Central to Penrose’s argument is his use of Gödel’s incompleteness theorem (Gödel 1931), which shows that there are truths provable by human reasoning but not derivable within any formal system. Extending this concept to multiple cognitive functions, Penrose suggests that humans are capable of recognizing patterns, making context-dependent decisions, and performing intricate physical tasks in ways that transcend formal algorithms. This capacity to grasp complex relationships, interpret subtle cues, and adapt actions in real-time aligns with the modern definition of hypercomputation, which refers to cognitive processes that exceed the power of a standard Turing machine.
A specific application of this idea is language, which serves as a fundamental model of human cognition. Language comprehension involves recognizing abstract meanings, interpreting context, and understanding metaphor and nuance — tasks that challenge the limitations of purely formal and algorithmic systems. Given that language engages core elements of human cognition, including abstract thought, symbolic representation, and context-driven adaptation, we argue that language itself operates as a hypercomputation. It showcases the ability to leverage non-computable insights and adapt in complex, nuanced situations that go beyond traditional models of computation.
Although Penrose did not explicitly use the term “hypercomputation,” his theory is consistent with its definition. He proposed that these advanced cognitive capabilities could arise from quantum processes within the brain’s microstructures, specifically within neuronal microtubules. According to Penrose, these quantum effects enable non-computable operations, which facilitate cognitive tasks that surpass the limitations of classical computation. Given that activities like language comprehension, precise motor control, and real-time decision-making are deeply intertwined with conscious thought, it is reasonable to conclude that these processes leverage the same non-computable mechanisms.
Thus, we claim that human cognition functions as a hypercomputation, informed by Penrose’s insights and the formal definition of the term. The specific case of language reinforces this broader claim, as it embodies many of the essential cognitive capabilities that exceed traditional computation. Penrose’s theory provides a strong foundation for this perspective, indicating that our cognitive processes operate at the intersection of advanced mental functions, quantum theory, and the limits of formal computational models.
4.5 Incompleteness of Infinite Time Turing Machines
While ITTMs extend the capabilities of classical Turing machines by introducing transfinite stages of computation, they are not exempt from their own intrinsic limitations. An ITTM can solve the halting problem for standard Turing machines by continuing computations through an infinite sequence of ordinal steps and evaluating the cumulative “limit state” reached. However, a crucial limitation emerges when considering the halting problem for ITTMs themselves, demonstrating that even these more powerful machines cannot entirely escape the implications of Gödel’s incompleteness theorem.
Gödel’s incompleteness theorem reveals that any sufficiently expressive formal system will contain true statements that are unprovable within that system. Applying this principle to ITTMs, which extend classical computation into the transfinite realm, we find that they must also encounter undecidable cases within their own framework. Just as a standard Turing machine cannot determine whether an arbitrary Turing machine will halt, an ITTM cannot determine whether an arbitrary ITTM will halt. The complexity introduced by infinite operations does not eliminate the fundamental constraints imposed by incompleteness.
The halting problem for ITTMs arises because, given the vast range of possible computations over transfinite ordinals, there will inevitably be configurations and sequences for which the ITTM cannot predict whether it will stabilize or continue indefinitely. Even though an ITTM can determine the halting behavior of classical Turing machines or lower-order computations, its capacity to analyze its own behavior remains limited. This mirrors Gödel’s insight that any system capable of expressing arithmetic contains statements about its own consistency and behavior that it cannot prove internally.
Therefore, while ITTMs can address the halting problem for conventional Turing machines, they encounter their own version of the halting problem due to the recursive nature of self-reference and the inherent incompleteness of formal systems. This limitation underscores that even within the more expansive framework of transfinite computation, the fundamental boundaries identified by Gödel still apply. Thus, the halting problem for ITTMs remains an unresolved question within their own extended computational framework, highlighting broader philosophical implications for the limits of computation and formal systems.
