2 Computation and the Turing Machine

The concept of computation, at its core, is a cornerstone of modern science and technology, underpinning everything from the devices we use daily to the theoretical frameworks that define the limits of what can be solved algorithmically. Central to this concept is the Turing Machine, introduced by Alan Turing in the 1930s (Turing 1936). This abstract and highly influential model provides a foundational framework for understanding computation, demonstrating how simple symbolic manipulations on an infinite tape can simulate the logic of any algorithm.

Turing Machines do more than serve as a theoretical construct; they encapsulate the principles of automata and complexity theory that form the backbone of computer science. Their elegance lies in their universality and simplicity, enabling profound explorations into the limits of computability, from decidable problems to the challenges posed by undecidability and computational complexity.

In this section, we delve into the mechanics of the Turing Machine, exploring how this deceptively simple model simulates algorithms and formalizes the essence of computation. We also examine how this framework has evolved, positioning the Turing Machine within a broader hierarchy of computational models, each with its unique capabilities and limitations. By doing so, we set the stage for understanding how foundational concepts of computation extend into more advanced paradigms, such as ITTMs, which challenge the boundaries of computability itself.

2.1 What is a Turing Machine?

Turing Machines (TMs) are a fundamental theoretical model in computer science to formalize the concept of computation. They serve as the foundation for understanding the limits of what can be computed and have profound implications for theoretical computer science, automata theory, and complexity theory. At its core, a Turing Machine is an abstract device that manipulates symbols on a tape according to a set of predefined rules, simulating the logic of any algorithm.

A Turing Machine consists of three primary components: an infinite tape, a read/write (R/W) head, and a transition rules table that governs the machine’s behavior. Each of these elements plays a vital role in defining the operation of the machine.

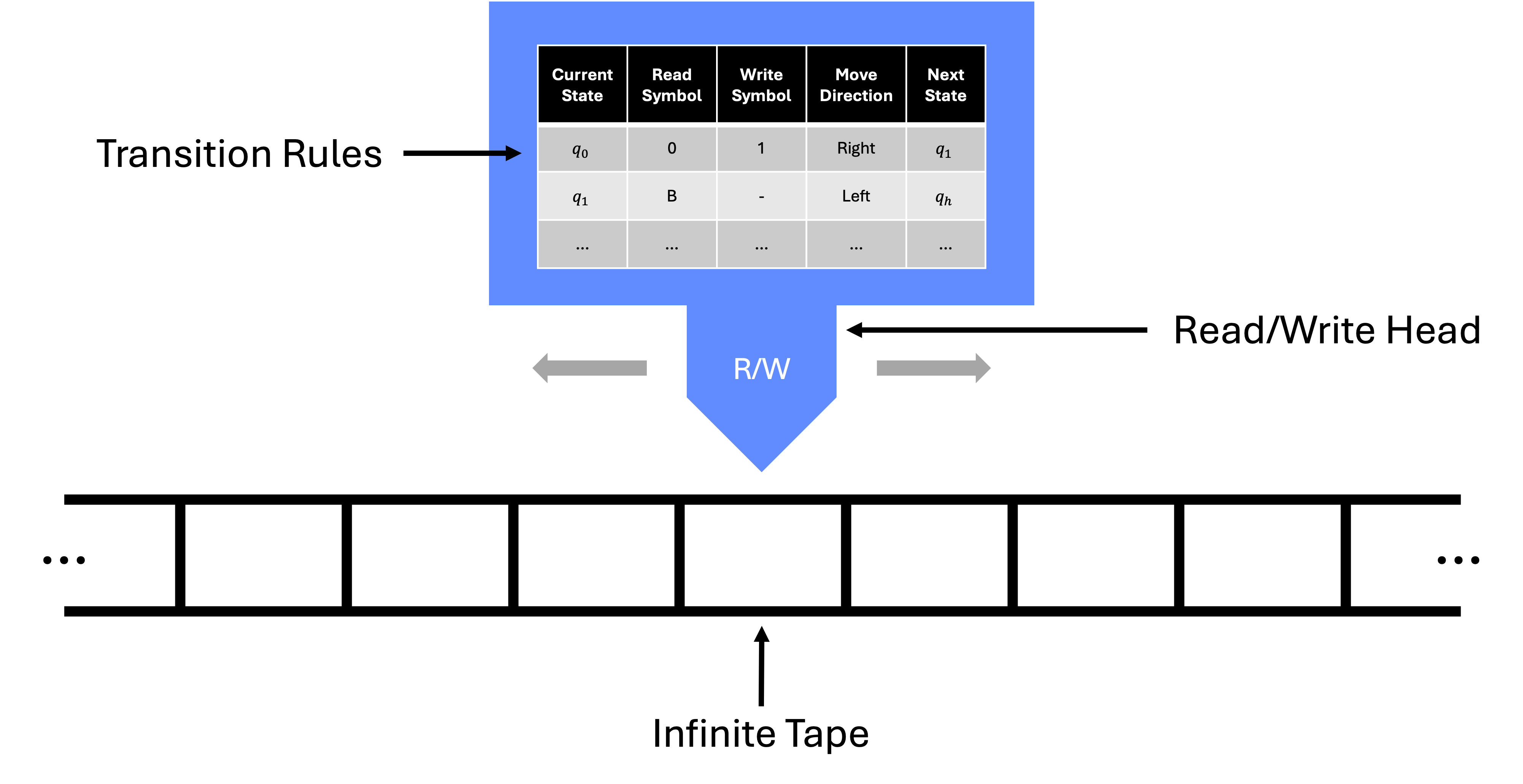
Figure 2.1: Depiction of a theoretical Turing Machine, highlighting key components

2.1.1 Infinite Tape

The tape is an infinite one-dimensional array that serves as the machine’s memory. Each cell of the tape can hold a single symbol, typically from a finite set known as the “tape alphabet.” At the start of computation, the input is written on the tape, and the rest of the cells are filled with a designated blank symbol.

The tape’s infinite nature is essential, as it allows the machine to continue processing without running out of space, regardless of the complexity of the computation. This abstraction allows Turing Machines to theoretically perform any calculation that could be completed by a modern computer with infinite memory.

2.1.2 Read/Write Head

The read/write (R/W) head is the mechanism that interacts directly with the tape. It moves along the tape, one cell at a time, reading the symbol in the current cell and writing new symbols as required by the machine’s rules. The head operates according to a set of instructions, determining whether to write a symbol, move left or right on the tape, or change the machine’s state.

The ability to both read and modify symbols is crucial, as it gives the machine the flexibility to adapt its computation based on intermediate results. The head’s movement is always controlled by the transition rules and can be either deterministic or non-deterministic, depending on the specific type of Turing Machine being considered.

2.1.3 Transition Rules Table

The transition rules table, also known as the machine’s “state transition function,” dictates the behavior of the machine. The table defines the set of operations the Turing Machine must perform based on its current state and the symbol it reads from the tape. Each rule specifies:

The current state of the machine.
The symbol currently under the R/W head.
The symbol to write in the current cell.
The direction to move the head (left or right).
The next state the machine should transition to.

The combination of these rules allows the machine to process the input on the tape and move towards either halting (completing the computation) or continuing indefinitely in the case of some undecidable problems. The transition function is finite, even though the tape and the possible number of computation steps are not.

In summary, a Turing Machine operates by manipulating symbols on an infinite tape via a read/write head, following a predefined set of rules contained in the transition table. This abstract model captures the essence of algorithmic logic and computation, making it a powerful tool for exploring the theoretical limits of computability.

2.2 Example: Binary Counter

To further illustrate the workings of a Turing Machine, we will use a simple example: constructing a binary counter. The goal of this Turing Machine is to increment a given binary number by 1. This example highlights how Turing Machines can perform arithmetic operations through symbol manipulation based on defined rules.

2.2.1 Goal: Increment Binary Numbers by 1

The objective of this Turing Machine is to take a binary number as input, and output the same number incremented by one. For example, given the binary number 11 (which is 3 in decimal), the machine should output 100 (which is 4 in decimal). This operation demonstrates the ability of a Turing Machine to simulate basic computational tasks such as addition.

2.2.2 Inputs and Outputs

The machine operates on binary numbers and produces corresponding binary outputs, similar to a counter. The process works for any binary number, increasing its value by 1 with each execution. For example:

Decimal Input	0	1	2	3	4	5	6	7	8	…
Binary Input	`0`	`1`	`10`	`11`	`100`	`101`	`110`	`111`	`1000`	…

2.2.3 Machine Alphabet

The machine operates on the binary alphabet and a blank symbol: {0, 1 B}, The blank symbol, B, is to represent the empty spaces on the tape beyond the input. The blank symbol ensures the machine can handle numbers of varying lengths without predefined tape limits.

2.2.4 Binary Counter Transition Rules

The transition rules for the binary counter Turing Machine are defined in the following table:

Table 2.1: Binary counter Turing Machine transition rules table.

Current State	Read Symbol	Write Symbol	Move Direction	Next State
\(q_0\)	0	0	R	\(q_0\)
\(q_0\)	1	1	R	\(q_0\)
\(q_0\)	B	B	L	\(q_1\)
\(q_1\)	0	1	-	\(q_h\)
\(q_1\)	1	0	L	\(q_1\)
\(q_1\)	B	1	-	\(q_h\)

The Turing Machine for this binary counter uses three distinct states to accomplish its goal:

\(q_0\) - Shift-Right: This is the initial state where the machine scans from left to right along the tape, searching for the rightmost 1 or 0. This state prepares the machine for the actual binary addition.
\(q_1\) - Carry: In this state, the machine performs the increment operation. It handles the logic of flipping 1 to 0 when a carry occurs, or writing 1 if the rightmost bit is 0.
\(q_h\) - Halt: This is the final state of the machine. It is reached after the binary number has been successfully incremented. At this point, the machine halts, leaving the updated number on the tape.

2.2.5 Example: Incrementing `11` to `100`

Consider the binary number 11 as input:

Starting Configuration: The machine begins at the leftmost position of the binary number in state \(q_0\). It moves right, scanning through the binary number until it finds the least significant 1 or 0.
Increment Process: Upon finding the rightmost 1, the machine transitions to state \(q_1\) (Carry) and flips this 1 to a 0, moving left if necessary to handle any carry bits. If a 0 is found, it simply changes the 0 to 1 and transitions directly to \(q_h\), the halt state.
Halting: Once the least significant bit has been updated, the machine transitions to state \(q_h\) and halts. The binary number on the tape will now reflect the incremented value, 100.

Figure 2.2: Binary Counter Turing Machine example, illustrating the process of incrementing `11` to `100`.

The final tape will contain the incremented binary number: 100. This process is depicted in Figure 2.2.

2.3 Hierarchy of Computation

The concept of computation can be understood as a spectrum, where different types of computational models are capable of solving problems of varying complexity. At the foundational level of this hierarchy are simple machines that can only handle basic tasks, while at the higher levels, more advanced machines can solve increasingly complex problems. Turing Machines, as introduced earlier, are a central model in this hierarchy. They form a baseline for defining computability, but they are part of a broader landscape that includes both simpler and more powerful machines.

This hierarchy can be ordered based on the computational power and complexity of the problems each machine can tackle, moving from less powerful models to more powerful ones:

2.3.1 Finite State Automata

Finite State Automata (FSA) represent the simplest computational model in this hierarchy. FSAs consist of a finite number of states and transitions between these states based on input symbols. They are capable of recognizing regular languages—those that can be expressed by regular expressions. However, their key limitation is the lack of memory beyond their finite state, meaning they cannot handle more complex structures such as nested or recursive patterns.

Computational Limitations: FSAs are limited to problems where the current state and input symbol alone are sufficient to determine the next action. They cannot process context-free languages or problems that require memory to track previously encountered input, such as balanced parentheses.

2.3.2 Pushdown Automata

Pushdown Automata (PDA) extend the power of Finite State Automata by incorporating a stack, which provides a form of memory. This allows PDAs to recognize context-free languages, which are a step more complex than regular languages. For instance, a PDA can recognize languages with nested structures, such as balanced parentheses, which an FSA cannot.

The stack allows the PDA to “push” symbols onto it or “pop” symbols off it, giving it the ability to remember an arbitrary number of past input symbols. However, the stack is a limited form of memory because it only allows for last-in, first-out access, which constrains the complexity of the problems PDAs can solve.

Computational Limitations: PDAs are not capable of solving problems that require more flexible forms of memory or full recursion, such as recognizing languages that are not context-free, including those with dependencies that go beyond simple nesting.

2.3.3 Turing Machines

Turing Machines, as discussed earlier, are a significant leap forward in computational power. Unlike PDAs, which use a stack, Turing Machines have an infinite tape that functions as both input and memory. This allows a Turing Machine to read, write, and move across the tape without the constraints of a stack-based structure.

Turing Machines can solve problems far more complex than those tackled by FSAs or PDAs. They are capable of recognizing recursively enumerable languages and can simulate any algorithm that can be executed on a modern computer. Turing Machines are the foundation of the Church-Turing thesis, which posits that anything that can be computed by an algorithm can be computed by a Turing Machine.

Computational Limitations: While Turing Machines are extremely powerful, they are still subject to certain limitations. For example, they cannot solve undecidable problems, such as the halting problem (determining whether a given program will halt or run indefinitely). Turing Machines are also limited by time and space complexity, which is why more advanced models have been proposed.

2.3.4 Oracle Turing Machines

Oracle Turing Machines extend the classical Turing Machine model by providing access to an “oracle,” a theoretical black box that can instantly provide answers to specific decision problems. The oracle can be thought of as solving problems that are beyond the computational limits of the Turing Machine itself, such as NP-complete problems.

With the help of the oracle, a Turing Machine can solve more complex problems, but the complexity of the problem that can be solved depends on the nature of the oracle. In essence, the oracle acts as a way to model more powerful types of computation that are not possible with a standard Turing Machine alone.

Computational Limitations: Oracle Turing Machines depend heavily on the nature of the oracle provided. They do not represent a practical model of computation but rather an idealized one that helps in classifying problem complexity (e.g., in complexity classes like P, NP, and beyond).

2.3.5 Infinite Time Turing Machines

ITTMs represent a further extension of computational power, designed to explore the boundaries of computation over infinite time scales. While classical Turing Machines are constrained by finite steps and time, ITTMs allow for an infinite number of computation steps, with specific rules governing behavior after “transfinite” time has passed. This provides a means to study problems that are not only undecidable by Turing Machines but that require computation over infinite time periods.

Computational Power: ITTMs can potentially solve certain problems that are unresolvable even by Oracle Turing Machines, as they can complete computations that would require an infinite number of steps. However, they also introduce new questions about the nature of computation in the realm of infinity, which we will explore in more detail in subsequent sections.

The hierarchy in Figure 2.3 illustrates the spectrum of computational models, where each level can handle progressively more complex problems. Finite State Automata and Pushdown Automata are limited by their simple memory structures, while Turing Machines and beyond can simulate increasingly sophisticated algorithms. By extending the classical Turing Machine model with infinite time, we can begin to approach problems that lie beyond standard computation, leading to deeper questions about the ultimate limits of what can be computed.